4 The Amorphous Kitaev Model
4 The Amorphous Kitaev Model
Contributions
The material in this chapter expands on work presented in
[1] Cassella, G., D’Ornellas, P., Hodson, T., Natori, W. M., & Knolle, J. (2022). An exact chiral amorphous spin liquid. arXiv preprint arXiv:2208.08246.
All the code is available online as a Python package called Koala [2].
This was a joint project of Gino, Peru and me with advice and guidance from Willian and Johannes, all authors of the above. The project grew out of an interest the three of us had in studying amorphous systems, coupled with Johannes’ expertise on the Kitaev model. The idea to use Voronoi partitions came from ref. [3] and Gino did the implementation of this. The idea and implementation of the edge colouring using SAT solvers and the mapping from flux sector to bond sector using A* search were both entirely my work. Peru produced the numerical evidence for the ground state and implemented the local markers. Gino and I did much of the rest of the programming for Koala collaboratively, often pair programming, this included the phase diagram, edge mode and finite temperature analyses as well as the derivation of the projector in the amorphous case.
Chapter Summary
In this chapter, I will first define the amorphous Kitaev (AK) model and discuss the construction of amorphous lattices. Second, in the methods section I will discuss the details of voronisation and graph colouring. Finally, I will present and interpret the results obtained.
From its introduction it was known that the Kitaev Honeycomb (KH) model is solvable on any trivalent lattice. Consequently, it has been generalised to many such lattices [4–7] but so far none that entirely lack translation symmetry. Here we will do just that.
Amorphous lattices are characterised by local constraints but no long-range order. They arise, for instance, in amorphous semiconductors like silicon and germanium [8,9]. Recent work has shown that topological insulating (TI) phases, characterised by protected edge states and topological bulk invariants, can exist in amorphous systems [10–16]. TI phases, however, arise in non-interacting systems. In this context, we might ask whether Quantum Spin Liquid (QSL) systems and the Kitaev Honeycomb (KH) model, in particular, could be realised on amorphous lattices. The phases of the KH model have many similarities with TIs but differ in that the KH model is an interacting system. In general, research on amorphous electronic systems has been focused mainly on non-interacting systems with the exception of amorphous superconductivity [17–21] or very recent work looking to understand the effect of strong electron repulsion in TIs [22].
The KH model is a magnetic system. Magnetism in amorphous systems has been investigated since the 1960s, mostly through the adaptation of theoretical tools developed for disordered systems [23–26]. This is not always ideal, we have already seen that the topological disorder of amorphous lattices can be qualitatively different from standard bond or site disorder, especially in 2D [27,28]. Research focused on classical Heisenberg and Ising models has accounted for the observed behaviour of ferromagnetism, disordered antiferromagnetism and widely observed spin glass behaviour [29]. However, the role of the spin-anisotropic interactions and quantum effects that we see in the KH model has not been addressed in amorphous magnets. It is an open question whether frustrated magnetic interactions on amorphous lattices can give rise to genuine quantum phases such as QSLs [30–33]. This chapter will answer that question by demonstrating that the Kitaev model on amorphous lattices leads to a kind of QSL called a chiral spin liquid.
In this section, I will discuss how to generalise the KH to an amorphous lattice. The methods section discusses how to generate amorphous lattices using Voronoi partitions of the plane [10,12], colour them using a SAT solver and how to map back and forth between gauge field configurations and flux configurations. In the results section, I will show extensive numerical evidence that the AK model follows the simple generalisation to Lieb’s theorem [34] found by other works [4–7]. I then map out the phase diagram of the AK model and show that the chiral phase around the symmetric point (\(J_x = J_y = J_z\)) is gapped and non-Abelian. We use a quantised local Chern number \(\nu\) [10,35] as well as the presence of protected chiral Majorana edge modes to determine this. Finally, I look at the role of finite temperature fluctuations and show that the proliferation of flux excitations leads to an Anderson transition, similar to that of the Falicov-Kimball model, to a thermal metal phase [36–38]. Finally, I consider possible physical realisations of the AK model and other generalisations.
The Model
The KH model is solvable on any lattice which satisfies two properties: it must be trivalent and it must three-edge-colourable. The first property means every vertex must have three edges attached to it [39,40]. 2D Voronoi lattices are a well-studied class of amorphous trivalent lattices [10,12,41]. Given a set of seed points, the Voronoi partition divides the plane into basins, based on which seed point is closest by some metric, usually the euclidean metric. The basins of each seed point form the plaquettes of the resulting lattices, while the boundaries become the edges. The Voronoi partition exists in arbitrary dimension \(d\) and produces lattices with degree \(d+1\) except for degenerate cases with measure zero [42,43]. Voronoi lattices in 2D are trivalent so lend themselves naturally to the Kitaev model.
Other methods of lattice generation exist. One can connect randomly placed sites based on proximity [11] or create simplices from random sites [44]. However, these methods do not present a natural way to restrict the vertex degree to a constant. The most unbiased way to select trivalent graphs would be to sample uniformly from the space of possible trivalent graphs. There has been some work on how to do this using a Markov Chain Monte Carlo approach [45]. However, it does not guarantee that the resulting graph is planar, which is necessary to be able to three-edge-colour the lattice, our second constraint.
The second constraint, three-edge-colourability, requires that we must be able to assign labels to each bond \(\{x,y,z\}\) such that no two edges with the same label meet at a vertex. Such an assignment is known as a three-edge-colouring. For translation invariant models we need only find a solution for the unit cell. This problem is usually small enough that this can be done by hand or using symmetry. For amorphous lattices, the difficulty is that, to the best of my knowledge, the problem of edge-colouring these lattices in general is in NP. To find colourings in practice, we will employ a standard method from the computer science literature for finding solutions of NP problems called a SAT solver, this is discussed in more detail in the methods secton.
We find that for large lattices there are many valid colourings. In the isotropic case \(J^\alpha = 1\) the colouring has no physical significance as the definition of the four Majoranas at a site is arbitrary. In the anisotropic case this symmetry is broken at the local level but we nevertheless expect the lattices to exhibit a self-averaging behaviour in larger systems such that the choice of colouring doesn’t matter.
On a lattice with the above properties, the solution for the KH model laid out in section 2.2 remains applicable to our AK model. See fig. 1 for an example lattice generated by our method. The main differences are twofold. Firstly, the lattices are no longer bipartite in general and therefore contain plaquettes with an odd number of sides which enclose flux \(\pm i\). This leads the AK model to have a ground state with spontaneously broken chiral symmetry [7,46–52]. This is analogous to the behaviour of the original Kitaev model in response to a magnetic field. One ground state is related to the other by globally inverting the imaginary \(\phi_i\) fluxes [47]. Secondly, as the model is no longer translationally invariant, Lieb’s theorem for the ground state flux sector no longer applies. However, as discussed in the background, a simple generalisation of Lieb’s theorem has been shown numerically to be applicable to many generalised Kitaev models [4–7]. This generalisation states that the ground state flux configuration depends on the number of sides of each plaquette as
\[\phi = -(\pm i)^{n_{\mathrm{sides}}},\qquad{(1)}\]
with a twofold global chiral degeneracy (picking either \(+i\) or \(-i\) in eq. 1).
To verify numerically that Lieb’s theorem generalises to the AK model, the obvious approach would be via exhaustive checking of flux configurations. However, this is problematic because the number of states to check scales exponentially with system size. We side-step this by gluing together two methods, we first work with lattices small enough that we can fully enumerate their flux sectors but tile them to reduce finite size effects. We then show that the effect of tiling scales away with system size.

In order to evaluate the Chern marker later, we need a way to evaluate the model on open boundary conditions. Simply removing bonds from the lattice leaves behind unpaired \(b^\alpha\) operators that must be paired in some way to arrive at fermionic modes. To fix a pairing, we always start from a lattice defined on the torus and generate a lattice with open boundary conditions by defining the bond coupling \(J^{\alpha}_{ij} = 0\) for sites joined by bonds \((i,j)\) that we want to remove. This creates fermionic zero modes \(u_{ij}\) associated with these cut bonds which we set to 1 when calculating the projector. Alternatively, since all the fermionic zero modes are degenerate anyway, an arbitrary pairing of the unpaired \(b^\alpha\) operators can be performed.
The Euler Equation
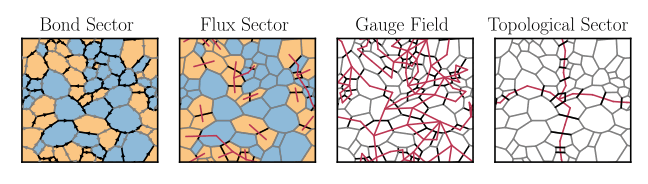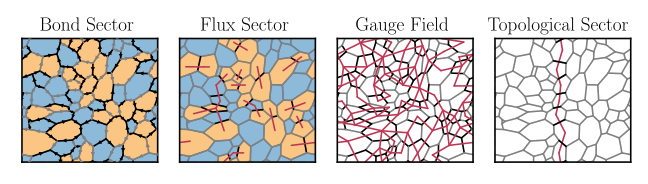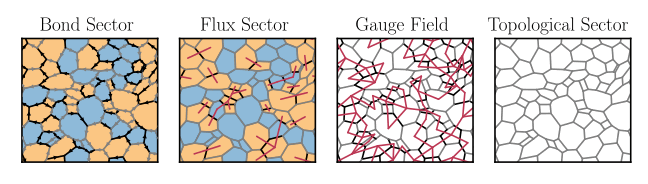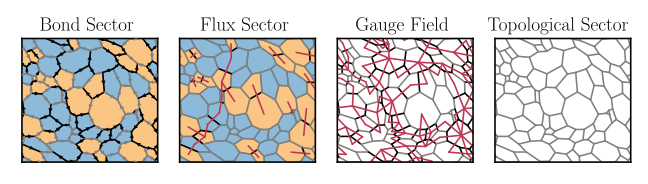
Euler’s equation provides a convenient way to understand how the states of the AK model factorise into flux sectors, gauge sectors and topological sectors as in fig. 2. The Euler equation states that if we embed a lattice with \(B\) bonds, \(P\) plaquettes and \(V\) vertices onto a closed surface of genus \(g\), (\(0\) for the sphere, \(1\) for the torus) then
\[B = P + V + 2 - 2g.\]
For the case of the torus where \(g = 1\), we can rearrange this and exponentiate it to read:
\[2^B = 2^{P-1}\cdot 2^{V-1} \cdot 2^2.\]
There are \(2^B\) configurations of the bond variables \(\{u_{ij}\}\). Each of these configurations can be uniquely decomposed into a flux sector, a gauge sector and a topological sector, see fig. 2. Each of the \(P\) plaquette operators \(\phi_i\) takes two values but vortices are created in pairs so there are \(2^{P-1}\) vortex sectors in total. There are \(2^{V-1}\) gauge symmetries formed from the \(V\) symmetry operators \(D_i\) because \(\prod_{j} D_j = \mathbb{I}\) is enforced by the projector. Finally, the two topological fluxes \(\Phi_x\) and \(\Phi_y\) account for the last factor of \(2^2\).
In a trivalent lattice, there are three bonds for every 2 vertices. Substituting \(3V = 2B\) into Euler’s equation tells us that any trivalent lattice on the torus with \(N\) plaquettes has \(2N\) vertices and \(3N\) bonds. Since each bond is part of two plaquettes this implies that the mean number of sides of a plaquette is exactly six and that odd sided plaquettes must come in pairs.
Next Section: Methods