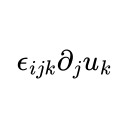Just a short thought. Lately I’ve been starting to read though these lecture notes on astrophysical fluid dynamics and this morning I came across this nice blogpost about numpy’s einsum function. Both reminded how lovely einstein summation is as a mathematical notation.

Here’s a quick intro to how it works and why it’s cool.

So Einstein notation usually comes up when you’re multiplying lots of high dimensional tensors together. Basically the idea is that you make summations implicit.

For example the definition of the product of two matrices $ A = BC $ can be written like this in terms of indices:

\[ A_{ik} = \sum B_{ij} C_{jk} \]

Here I’ve left off the sum limits because you usually know them from context or they can be defined later. For example here we could add that this equation only makes sense if A, B and C are of shapes (m, l), (m, n) and (n, l) respectively. So we know the sum should be over n indices.

Einstein summation notation is basically the statement “Whenever you see a pair of indices in an expression, pretend their is a sum over that index (over the appropriate range)”. With this, the above equation becomes:

\[ A_{ik} = B_{ij} C_{jk} \]

You can find really good expositions of this online so I won’t go into more basic detail here but here is a list of nice quality of life improvements you can add on top of this.

Div, Grad, Curl

In Vector calculus you deal with a lot with partial derivatives $\tfrac{\partial}{\partial \alpha}$ where $\alpha$ can be x, y, z, or t. My first hack is that you should start writing your partial derivatives as $\partial_\alpha$ instead. Then div, grad and curl become quite succinct:

Div: \[ \nabla \cdot \vec{u} \rightarrow \partial_i A_i \]

Grad: \[ \nabla \vec{u} \rightarrow \partial_i u_j \]

Curl: \[ \nabla \times \vec{u} \rightarrow \epsilon_{ijk} \partial_j u_k \]

Where these indices implicitly sum over x, y, and z.

That $\epsilon$ is the Levi-Civita symbol.

Spacetime

In relativity, space and time get put on a more equal footing. They’re not the same exactly but it makes sense to start to let our indices run over both space and time. Though there are occasions where we would like to just run over space too. The first hack for this is we say that indices from the Greek alphabet should be read as running over t, x, y, and z while those from the Latin alphabet run over just the spatial indices as before.

This lets us take something like a continuity equation

\[\partial_t \rho + \nabla \cdot \vec{u} = 0 \]

which expresses the idea of conservation of ‘stuff’ if $\rho$ is a density field of stuff and $\vec{u}$ is its velocity field, and transform it to:

\[ \partial_\mu v_\mu = 0 \]

where $v = (\rho, \vec{u})$ is called a 4-vector and nicely packs up the very closely related concepts of $\rho$ i.e “how much stuff is right here” and $\vec{u}$ i.e “where is the stuff here flowing to?”.

You can do similar tricks for many physical quantities such as charge and current, the magnetic field and the electric field, energy and momentum etc.

Flat and curved spacetime

This next bit starts to touch on things beyond my ken but I’ll gesture at it anyway.

When you start to talk about curved space and even spacetime it becomes useful to define a special two dimensional tensor called the metric. In flat spacetime the metric is called ‘the Minkowski metric’ and it’s a diagonal matrix $\eta_{\mu\nu}$ with (1, -1, -1, -1) along the diagonal. It could also be (-1, 1, 1, 1) if you like.

Now for flat spacetime the metric really just helps us keep track of signs. The simplest place it crops up is that the ‘spacetime interval’ between two events in space and time is:

\[ \delta s^2 = \delta t^2 - \delta x^2 - \delta y^2 - \delta z^2 = \delta_\mu \eta_{\mu\nu} \delta_\nu \] or \[ \delta s^2 = \vec{\delta} \cdot \eta \cdot \vec{\delta} \]

For curved spacetimes, the metric gets more complicated and can have arbitrary off diagonal terms too which describe the curvature of spacetime and other effects.

The final trick is that this insertion of the metric in the middle of tensor contractions comes up so much that we can define a new notation just for it, we say that when you contract a superscript index with a subscript index, you have to insert the metric in between:

\[\delta^\mu \delta_\nu = \delta_\mu \eta_{\mu\nu} \delta_\nu \]

Now I’ve called these things hacks and tricks but they also connect to much deeper mathematical concepts such as covariance and contravariance. This seems like it’s usually the case with nice notation. It makes me think things like the relationship between the derivative operator $\tfrac{d}{dt}$ and and the infinitesimal $dt$.

np.einsum

einsum is a nice cross over between the theoretical math world and the get stuff done world of numerical programming. Because arrays in numpy know how many dimensions they have and how big they are they lend themselves naturally to the einstein summation syntax. The way this is implemented in numpy is that you pass your tensors to the function along with a special string that tells einsum how to contract the indices together.

Taking the simple matrix multiply again as a an example:

\[ A_{ik} = B_{ij} C_{jk} \]

Becomes:

import numpy as np

B = np.array([[0,1], [1,0]])
C = np.array([[1,3], [2,4]])

A = np.einsum("ij, jk", B, C)
A

You can see how the ij are the indices of B, jk those of B and how this would generalise to more tensors or tensors with more dimensions. This is the implicit mode of einsum, in this mode it basically follows the normal einstein summation rules of contracting pairs of indices. And in those rules certain things are not allowed, the same index is not allowed to appear three times for example, nor can we express something like an elementwise multiplication of two matrices in normal einstein summation. To be fair such operations are relatively rare, so you can get around it by just writing “for this equation don’t sum over i”.

But einsum has an explicit mode that lets use express some of these operations:

import numpy as np
B = np.array([[0,1], [1,0]])
C = np.array([[1,3], [2,4]])

np.einsum("ij, jk -> ik", B, C)

Using the -> we can also express the indices of the output tensor. Using this we can express the element wise product of two matrices too:

import numpy as np
B = np.array([[0,1], [1,0]])
C = np.array([[1,3], [2,4]])

np.einsum("ij, ij -> ij", B, C)

which I guess would be equivalent to the equation:

\[ A_{ij} = B_{ij} C_{ij} \; \text{(No sum over indices)}\]

I used this to generate the thumbnail for this post.