I wanted my thesis to have a nice HTML version in addition to the mandatory-in-my-field latex/PDF version. Having a HTML version also means I can experiment with a bit of interactivity. I’ve done some of the diagrams in SVG using Inkscape which is a nice tool for this kind of thing. I wanted to add some interactivity as an easter egg to the SVGs in the HTML version.

How hard could that be? It turns out harder than I expected!

On changing web standards

Disclaimer: The web is an evolving thing. Depending on when you read this some of what I saw here may already be out of date, or the workarounds needed might be fixed on some browsers. This is your reminder to check the date of this post before trying to copy anything in here, something I forget to do often.

The first hurdle is how you embed your SVG files in your HTML. For HTML version of the thesis I’ve been using img tags inside figure tags like this

<figure>
<img src="/path/to/image.svg"/>
<figcaption>
Figure 3: Caption goes here!
</figcaption>
</figure>

I like this setup. It uses semantic HTML tags which give useful hints to screen readers about how to interpret this content non-visually. The problem here is the img tag. Embedding SVGs this way will display them nicely but the SVG elements won’t be available to an JS running on the page. This is because when the browser sees an SVG loaded through an img and renders it as a static image. This also means you can’t select the text or other elements in the SVG!

So what’s the alternative? Well if you google how to embed svgs you’ll see that you have a few options: object tags, svg tags, iframe tags etc. I had a play around with a few of these options but because I am generating my HTML from markdown via pandoc, it’s a little tricky to use entirely custom HTML. The best option for interactivity seems to be embedd the svg directly into the HTML in an svg tag. I don’t like this so much because it fills my nice HTML files up with hundreds of lines of SVG and means it’s not so easy to edit them in inkscape with a tedious copy paste step.

In other pages on this blog I solved this using Jekyll. Jekyll is a static site generator and it’s easy to tell it to take the contents of a file like myimage.svg and dump the contents into the HTML at compile time.

For the thesis however I’m using pandoc and targeting both HTML and latex. In principle I could have written a pandoc filter to replace img tags that link to .svg files with raw SVG but I didn’t want to add any more complexity to that build system just for a small easter egg. I didn’t even need to do this for all teh SVGs, just the ones I wanted to add interactivity too.

Instead I chose to stick with the img tags but use some JS to dynamically replace them with svg tags when I wanted to add interactivity. I query for the image I want, use d3.xml to download the content of the src attribute, and then replace the img with the constructed svg tag.

 //grab the img tag containing our target svg
 const img = document.querySelector("img#id-of-image");
         
 if(img !== null) {
     d3.xml(img.getAttribute('src')) //download the svg
         .then(data => {
             const svg = data.documentElement;
             svg.setAttribute('width', '100%');
             svg.setAttribute('height', 'auto');
    
           d3.select(img).node().replaceWith(svg);
    });
}

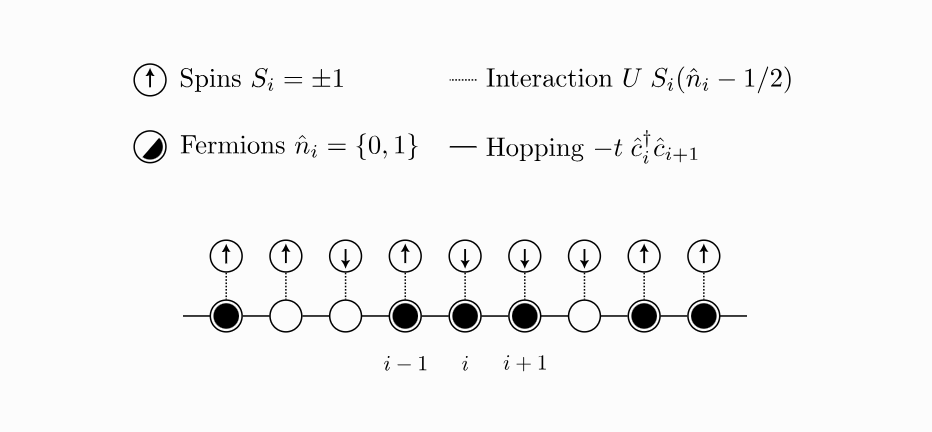
My target image looks like this

This diagram represents a model of a quantum system of spins and fermions. The spins are the little arrows which can either be up or down and the fermions are the little circles which can either be filled or unfilled. I want to make both of them switch states when you click them.

Fermions

First we need a way to select the fermions with d3, this is where the xml editor in inkscape comes in. With Edit \> XML Editor you can add attributes to any SVG element using the little “+” icon. I used this to add “class : fermion” to each of the fermion circles.

Now to animate them with d3, after a false start involving trying to figure out how to reliably compare colours in d3 I switched to using opacity and ended with with this code:

const fermions = d3.select(svg).selectAll(".fermion");
fermions.on("click", function() {
    d3.select(this)
        .transition()
        .duration(100)
        .style("fill-opacity" , d => {return d3.select(this).style("fill-opacity") === '1' ? 0 : 1});
}, true)

The trick here is that in d3 you can set attributes with a function and use d3.select(this) to get a handle on the current element. You can then do a query on the current value of the style and change it accordingly. Originally I had wanted to switch the fill colour between black and white but try as I might I could not find a way to reliably compare two colours together.

Spins

Same deal for the spins, add a class: spin to them all using the XML editor.

I had originally wanted them to animate a nice rotation, but I couldn’t find an eay way to compute the geometric centre of each spin to rotate about. I had a go with transform-origin: centre but couldn’t get it to work.

So I use a different hack, I switched when end of the line the arrow head is on:

 const spins = d3.select(svg).selectAll(".spin");
 spins.attr("pointer-events", "all"); //this is the subject of the next paragraph!
 spins.on("click", function() {
     const start = d3.select(this).select("path").style("marker-start");
     const end = d3.select(this).select("path").style("marker-end");
     const direction = (start === "none");
     const url =  direction ? end : start;
 
     d3.select(this).select("path")
        .transition()
        .duration(100)
        .style("marker-start", () => {return direction ? url : "none"})
        .style("marker-end", () => {return direction ? "none" : url})
}, true)

After this, I could make the spins flip but only if I clicked in a very tiny area near each spin. It turns out that this is because the default way for SVG elements to determine if you’ve clicked on them is a bit conservative. Adding spins.attr("pointer-events", "all"); fixes this.

Finally we end up with this:

You can also see it in context in the introduction to my thesis.